В предыдущей статье мы продемонстрировали, что менискообразная форма шва вызывает чрезмерное растяжение в центральной тонкой части шва. Деформация герметика в этом опасном сечении будет больше той, которой подвергается сам шов и на которую рассчитан герметик. Мы указали, что "без всяких "умных" формул" разрушается "привычное представление о преимуществах вогнутого шва" и отметили, что "тезис про вогнутость еще проще опровергается с помощью "умных" формул". Мы вернулись к этой теме, потому что представление об обязательном наличии "мениска" в шве герметика еще существует в строительном мире. Для инженеров-проектировщиков зачастую непривычно, что плоский шов долговечнее менискообразного. Поэтому мы приводим строгий расчет для доказательства нашей позиции и демонстрируем эти "умные" формулы.
Постановка задачи
В данном случае деформацию слоя герметика мы будем оценивать через его относительное удлинение. В практике это понимается как отношение изменения ширины шва к первоначальной ширине. Назовем это отношение "кажущейся деформацией" шва. При неравномерной толщине шва – например, при исполнении шва в форме "мениска" – отдельные его части будут испытывать разную деформацию. Поэтому уместно ввести понятие "истинной деформации" шва как деформации опасного сечения. Если истинная деформация больше кажущейся деформации, то это отличие важно учитывать при проектировании и исполнении монтажных, фасадных и других строительных швов. Таким образом, цель данного расчета состоит в оценке отношения истинной и кажущейся деформации для менискообразного шва.
Расчет
Исходя из рекомендаций для конструкционных швов примем, что ширина шва L в два раза больше минимальной толщины h (Рис.1).
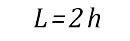 (1)
(1)
Локальную толщину H шва будем находить из формы кривой, которая определяет "мениск". Начало системы координат расположим в центре поперечного сечения шва, ось z направим вдоль ширины шва. Будем считать, что шов ограничен симметричными дугами окружностей некоторого радиуса R, что соответствует условию:
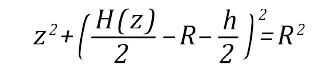
Тогда получаем уравнение верхней границы шва в виде:
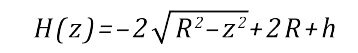
Или, с учетом (1)
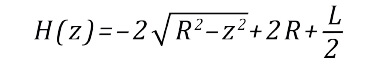 (2)
(2)
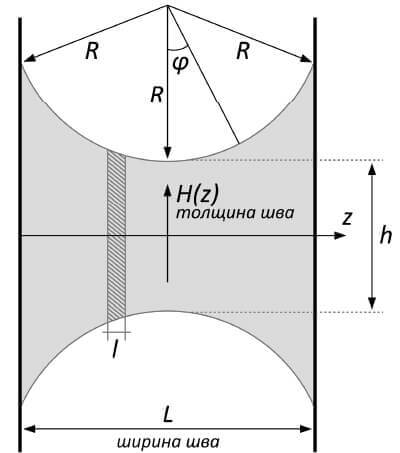
Рисунок 1. Типовая схема конструкционного шва
Мысленно разобьем шов на тонкие слои. Согласно закону Юнга относительное удлинение ε каждого слоев составляет
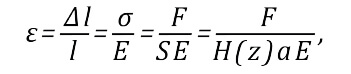 (3)
(3)
- где l – ширина рассматриваемого слоя шва (см. Рис.1),
- ∆l – его абсолютное удлинение,
- F – сила, растягивающая шов,
- σ – возникающее в данном слое напряжение,
- E – модуль Юнга,
- S – площадь поперечного сечения данного слоя,
- z – положение центра слоя во введенной системе координат,
- a – длина шва в направлении, перпендикулярном рисунку.
Удлинение шва ∆lΣ складывается из удлинения его отдельных сечений, поэтому рассчитаем ∆lΣ интегрированием локальных деформаций по ширине шва. Растягивающее усилие F для всех слоев шва одинаково: в противном случае происходило бы движение слоев под действием разницы сил натяжения, действующих на левые и правые стороны. При переходе к дифференциально малым слоям начальную ширину слоя l обозначим как dz:
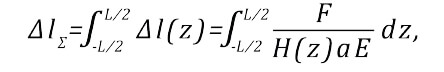
где ∆l(z) – удлинение дифференциально малого слоя шва.
Подставляя полученное ранее выражение для толщины шва (2), получим:
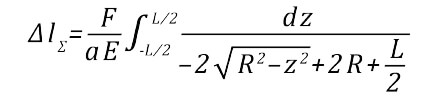
Данный интеграл можно взять аналитически, выполнив сначала переход от интегрирования по z к интегрированию по углу ϕ (Рис. 1), а затем универсальную тригонометрическую подстановку. Получим
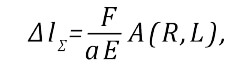
где
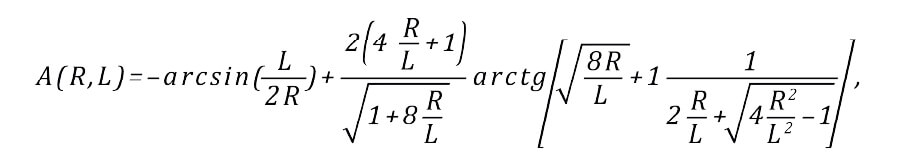
Откуда
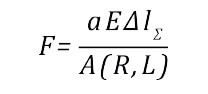
Из (3) следует, что максимальное относительное удлинение развивается в сечении с минимальной толщиной шва H(0)=h. В этом критическом сечении деформация составит
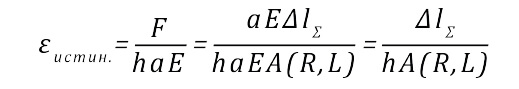 (4)
(4)
Для шва постоянной толщины растяжение на ∆lΣ вызывает равномерное относительное удлинение всех слоев на:
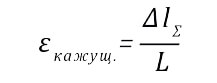 (5)
(5)
Из (4) и (5) с учетом (1) искомое отношение истинной и кажущейся деформаций для шва в форме мениска составляет:
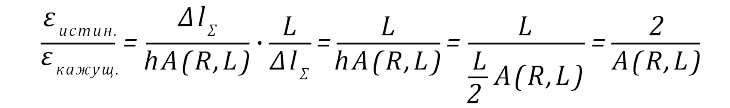 (6)
(6)
При R → ∞ рассмотренный менискообразный шов превращается в шов равномерной толщины, а выражение (6) действительно становится равным единице. При уменьшении R выражение (6) растет, достигая максимума при минимально возможном R:
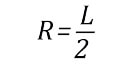 (7)
(7)
тогда
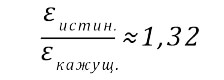
Получается, что если заложить в проект деформацию монтажного шва в 15%, то при использовании "мениска" (с размерами, соответствующими (1) и (7)) истинная деформация будет равна 1,32 × 15% ≈ 20%. Таким образом, использование менискообразной формы шва увеличивает истинную деформацию и, следовательно, уменьшает срок службы шва. Насколько именно? Исследования на акриловых герметиках не проводились, но для полиуретановых герметиков, которые применяют в высокодеформативных швах, повышение амплитуды деформации в среднем пропорционально уменьшает срок службы герметика. Если для акриловых герметиков сохраняется такая же зависимость, то менискообразный монтажный шов при заданных параметрах прослужит на 25% меньше, чем плоский.
Выводы и лирическое отступление
Итак, с помощью "умных формул" мы подтвердили, что тонкое сечение при использовании менискообразной формы шва испытывает повышенные нагрузки. Отметим, что некоторые производители монтажных лент не оставляют попыток навязать использование забутовочных шнуров (а, значит, и "мениска") при использовании герметиков, потому что "так делают в Европе". Расчет показывает, что такая позиция неверна. Можно было бы предположить, что такое стремление вызвано единственно желанием упомянутых производителей получить конкурентное преимущество1, но мы считаем, что в данном случае это не так. Они попросту заблуждаются.
1 Ведь монтаж на герметики становится при использовании шнуров сложнее и, главное, дороже, чем монтаж на ленты.